Tokenization in large language models, explained

Modern language models predict "tokens", not words—but what exactly are tokens?

In April, paying subscribers of the Counterfactual voted for a post explaining how tokenization works in LLMs. As always, feel free to subscribe if you’d like to vote on future post topics; however, the posts themselves will always be made publicly available.

---

Large Language Models (LLMs) like ChatGPT are often described as being trained to predict the next word. Indeed, that’s how I described them in my explainer with Timothy Lee.

But that’s not exactly right. Technically, modern LLMs are trained to predict something called tokens. Sometimes “tokens” are the same thing as words, but sometimes they’re not—it depends on the kind of tokenization technique that is used. This distinction between tokens and words is subtle and requires some additional explanation, which is why it’s often elided in descriptions of how LLMs work more generally.

But as I’ve written before, I do think tokenization is an important concept to understand if you want to understand the nuts and bolts of modern LLMs. In this explainer, I’ll start by giving some background on what tokenization is and why people do it. Then, I’ll talk about some of the different tokenization techniques out there, and how they relate to research on morphology in human language. Finally, I’ll discuss some of the recent research that’s been done on tokenization and how that impacts the representations that LLMs learn.

For anyone interested in learning more, I also highly recommend the tutorials on tokenization produced by HuggingFace, the company responsible for the widely-used transformers library in Python.

What are “tokens” and what are they good for?

LLMs are predictive models. That is, they are trained to predict elements in a sequence, based on the other elements that appear in that sequence. Tokenization is the process of breaking up that sequence into a bunch of discrete components (“tokens”). These tokens, in turn, can be viewed as the model’s vocabulary—the kinds of things that a model is trained to recognize and produce. In order to train and use the LLM, we have to make some decisions about what goes into its vocabulary.

To contextualize this a bit, let’s consider a simple sequence of words, with the final word missing:

The quick brown fox jumped over the lazy ___

Reading this sentence, it’s clear to us what the words are. But to a computer, a block of text (a “string”) is just one long sequence of characters. By default, a computer program doesn’t know what a word is; for example, in Python, a string is actually represented by a series of Unicode characters. If we want a system to predict the next “element” in that sequence, we first have to decide what kind of thing those elements are and how to identify them in the text. Are the elements words? Individual characters?

A natural place to start is to chunk the sequence into words. In a language like English, written words are typically separated by spaces, so identifying the word boundaries is pretty straightforward (this is not the case in every language!). We can divide the string along each space character we find, producing a list of “words” (the non-space characters). Programming languages like Python offer a number of ways to do this, and packages like the Natural Language Toolkit (nltk) have useful functions that can make our lives easier. The ultimate goal is to produce something like this:

['The', 'quick', 'brown', 'fox', 'jumped', 'over', 'the', 'lazy']

That list of words is a tokenization of the sentence we started with. Each unit in that sequence is a token, which in this case corresponds to the words in that sentence. A language model can use those tokens to determine what token is most likely to come next. Technically, each token is assigned a different ID; in modern LLMs, these IDs map onto a token embedding, which in turn is fed into the LLM. (For more details on how LLMs and embeddings work, I recommend my explainer with Timothy Lee.) These unique IDs are simply numbers. To illustrate what this might look like, I tokenized the sentence above using the same tokenizer that BERT (a language model created by Google) uses:¹

[1996, 4248, 2829, 4419, 5598, 2058, 1996, 13971]

Note how at least one of those IDs repeats: “1996” is the ID assigned to the word “the”, which occurred twice in the sentence. As I mentioned above, each of these IDs maps onto a unique embedding in the BERT language model. To make a prediction about what word comes next, BERT looks up each of those embeddings and runs them through the model’s layers.

Tokenization is a crucial step for training a language model because it determines a model’s vocabulary. A language model needs to “know” how to process its input and what kinds of things it’s supposed to predict. For example, if we want our model to pay attention to words and produce words, then the model must know what the words are and how to identify them. One way to think about this is that tokenization tells the model what kinds of things exist in the first place. This is why historically, handling unknown or “out-of-vocabulary” (OOV) words was a big problem for language models: if a token isn’t the model’s vocabulary, how would it know to produce that token or assign it some probability in the context of other tokens? Computational linguists have devised all sorts of techniques to handle unknown words, e.g., assigning them some constant, low probability.

Of course, we could’ve decided that our tokens should be characters, not words, in which case the tokenization for the original sequence would’ve looked like this:

['T', 'h', 'e', ' ', 'q', 'u', 'i', 'c', 'k', ...]

Such a language model would be character-based, as opposed to word-based. That means that the language model is trained to predict (and generate) individual characters.

Training a model to predict characters instead of words has some advantages. First of all, there are many fewer possible characters than words; that means the model’s vocabulary can be much smaller than if it were based on words. Similarly, training on characters rather than words gives a model much more flexibility. Even if the model has never observed a particular sequence of characters, it’s probably observed the individual characters in that sequence, so it can still assign that sequence some probability. This flexibility is well-suited to handling OOV words, but it comes at a cost. Many predictions in language depend on previous words or even syntactic phrases, and focusing on individual characters is so low-level that it makes it more challenging to learn about those higher levels of abstraction. It also means the models’ context window has to be quite a bit longer: if you want to know what word occurred three words ago, a word-based model only needs a context window of three tokens, while a character-based model probably needs a context window of at least 14 tokens (since English words have about 4.7 characters on average).

So: tokenizing by spaces results in a huge vocabulary with less flexibility, and tokenizing by characters makes the actual language modeling task harder. These days, language models use a kind of hybrid approach that’s meant to incorporate the best of both worlds. This approach is called subword tokenization.

The rise of subword tokenization

Subword tokenization is based on the observation that words are, by definition, composed of smaller substrings (“subwords”) that recur across lots of other words. The smallest possible substring in a word is, of course, a character (e.g., “d”). But longer substrings might be useful to identify too, especially if they’re frequent enough that they can be found in other words.

To illustrate what this looks like, I used BERT’s tokenizer to find examples of two-syllable words that were decomposed into two (as with “racket”) or even three (as with “vanquish”) tokens. Here, the “##” notation indicates that this token is a subword token in BERT’s vocabulary. The “##et” token will be assigned its own embedding, just like whole words like “lesson”.

Examples of different two-syllable words tokenized using BERT’s tokenizer.

What determines whether a word will be represented with a single token or decomposed into smaller, common subwords? As the HuggingFace tutorial explains, it’s all about frequency. If a word is extremely frequent, the tokenizer will probably use a single token to represent it. But if a word is less frequent, the tokenizer might not bother adding the whole word to its vocabulary—instead, it will rely on decomposing the word into more common subwords. This can sometimes result in some weird tokenizations, as with “vanquish” above, but the hope is that it helps modern LLMs navigate the Scylla and Charybdis of word-based and character-based models.

In practice, there are a few different subword tokenization techniques. Most of them operate according to a similar principle (use a single token for common words, and use multiple tokens for less common words), but are implemented in slightly different ways.

One popular technique is called byte-pair encoding (BPE). BPE starts out by creating tokens for all the basic symbols used in a tokenizer’s training text, e.g., individual characters like “d” or “o”; this is analogous to a character-based model’s vocabulary. Then, BPE searches for ways to start merging these basic symbols into common strings. A “merge” operation simply refers to combining two tokens that already exist in the model’s vocabulary. At first, these tokens will be individual characters, so merging will create two-character tokens: for example, the characters “d” and “o” may be combined to create the substring “do”, if such a substring is sufficiently common. That means the model’s vocabulary would now include individual characters, as well as the substring “do”. Later, these longer substrings can be used in merge operations as well: for example, the substring “do” may be combined with the character “g”, meaning that the model’s vocabulary would now include the string “dog” as well.

This process is applied until some predetermined vocabulary size is attained. For example, a researcher might decide that they want a vocabulary no larger than 50,000 tokens. That means that BPE would keep merging different tokens and adding new items to the vocabulary up to the point where the vocabulary already has 50,000 tokens. Once the desired vocabulary size is reached, tokenization is complete and language model training can begin in earnest.

In practice, decisions about the model’s vocabulary size mostly come down to performance. Larger vocabularies allow for more specific word (or subword) representations, but they also result in larger (and often slower) models. Thus, researchers have to balance the demands of lexical coverage (how many words the tokenizer “knows”) and efficiency (how easily and quickly the model can be trained and run). Subword tokenization isn’t a panacea, but at least in contemporary LLMs, it does generally work better than explicitly character-based or word-based tokenization.

Are subwords the same thing as morphemes?

If any linguists are reading this post, all this discussion about “frequent subwords” is probably making you think about morphemes. A morpheme is defined as the smallest meaningful unit of an expression. Some words have only one morpheme (e.g., “dog”), while others have multiple morphemes (e.g., “dogs” = “dog” + “-s”). Morphemes are productive, which means that they can be combined together to create new words with systematic, predictable meanings. For example, the suffix “-s” can be added to a number of different English nouns to indicate that the noun is plural.

Morphology is an example of compositionality, which is part of what makes human language so powerful. Instead of creating an entirely new word to mean “more than one dog”, we can simply glue together the root word (“dog”) with a plural suffix (“-s”). In principle, that should reduce the number of different words or morphemes we need to remember, and it should also give us more flexibility when producing novel expressions; importantly, it also probably makes those novel expressions easier to understand, since a language comprehender can figure out that “dogs” is just “dog” and “-s” put together, i.e., “more than one dog”.²

Morphology also plays an important role in language learning, and there’s been lots of research investigating how and when children acquire an understanding of morphology. A classic 1958 study conducted by Jean Berko found that children as young as 3-5 were able to generalize morphological rules (like the plural “-s”) to novel words they’d never seen before, like “wug”.

Example “wug” and “wugs” from Jean Berko’s classic 1958 study.

These benefits seem pretty similar to the purported benefits of subword tokenization, so it’s tempting to think that subword tokenization is implicitly learning morphology—except that’s not really true.

If subword tokenization worked by decomposing words into their morphemes, then words like “dog” would be represented with a single token, while words like “dogs” would be represented by multiple tokens. In practice, that’s not what happens: both words are represented by single tokens. In contrast, single-morpheme words like “racket” are represented as two tokens (“rack” + “##et”). That’s because subword tokenization isn’t trained to identify morphemes—it’s trained to identify the most frequent subwords, which may or may not correspond to morphemes.

In some cases, subword tokenization converges upon morphemes incidentally. For example, the “de-” in “dehumidifier” is represented as its own token (see below).

'de', '##hum', '##id', '##ifier'

At the same time, the root “humid” is actually represented as two tokens when it occurs in “dehumidifier”, even though on its own, “humid” is represented as a single token! That’s because the tokenizer learned a representation for “humid” on its own, but apparently not for when it occurs in the middle of a string. And technically, a morphological parse of “ifier” would probably be two morphemes: “-ify” and “er”.

A quick, informal analysis suggests that the prefix “de-” is often identified as a separate token (e.g., as in “decompose” or “deactivate”). Yet, as with “dehumidifer”, the root words are not always represented as single morphemes either (e.g., “decompose” is tokenized into “de” + “##com” + “##pose”).

In answer to the question heading this section, then, subwords are not the same thing as morphemes. If we’re feeling generous, we might think of subwords as “morphemes for language models”, though I’m not sure whether such an analogy is helpful or not. But the subwords that algorithms like BPE learn often don’t map onto the morpheme boundaries of human language and have no intrinsic meaning—at least to us humans.

How much does morphology matter?

Morphology is an important part of human language. Since subword tokenization doesn’t guarantee that words are tokenized according to morpheme boundaries, one might think that this could impair the ability of a language model to learn useful representations. Is this true? And if so, does training tokenizers according to morpheme boundaries help?

Notably, there has been increasing interest in what’s called “morphologically aware” tokenization. These approaches encourage tokenizers to learn subword tokens that correspond to morphemes, as opposed to simply learning the most frequent subwords. One way to do this is to start with a list of the known morphemes in a language (and how different words decompose into those morphemes), and force the tokenizer to start with those morphemes.

From one perspective, modern LLMs are already pretty impressive—which implies that maybe subword tokenization is working just fine. At the same time, most popular LLMs are built for languages like English, which have relatively simple morphology. In contrast, synthetic languages like German have famously complex morphology, which could pose more of a problem for non-morphemic tokenization schemes. Further, as this recent preprint makes clear, there simply hasn’t been enough analysis of exactly how distinct tokenization schemes impact downstream performance. For example, one might expect morphologically aware tokenization to be particularly helpful when an LLM must generalize to out-of-vocabulary words consisting of multiple morphemes. For example, if the word “deactivate” was not in an LLM’s vocabulary, it seems like the LLM would have an easier time representing that novel word if it was tokenized according to known, meaningful tokens (“de” + “activate”), rather than somewhat random subwords that don’t have meaning on their own (“deac” + “tivate”).

From what I’ve read, evidence is kind of mixed on whether and how the lack of morphology in subword tokenizers impairs model performance.

In a recent workshop paper, I investigated this question along with three co-authors at UC San Diego (Catherine Arnett, Pam Rivière, and Tyler Chang). We focused on the phenomenon of article-noun agreement in Spanish. In Spanish (as in many languages), the number of the article must “agree” with the number of the noun (e.g., “la mujer” vs. “las mujeres”). We asked how well a pre-trained Spanish language model could predict the correct article (e.g., “la” vs. “las”) from a noun. Crucially, we also asked whether the LLM’s ability to do this was dependent on whether the noun was tokenized according to morpheme boundaries. This was especially relevant for plural nouns: in some cases, plural nouns were tokenized as whole words (“e.g., “mujeres” —> “mujeres”), while in others they were tokenized according to morpheme boundaries (e.g., “naranjas” —> “naranja” + “##s”), and in still other cases they were tokenized into non-meaningful subwords (e.g., “neuronas” —> ““neuro” + “##nas”). (e.g., “mujeres”).

Somewhat surprisingly, we found that the way the noun was tokenized didn’t really have a meaningful impact on the LLM’s ability to predict the correct article—even when controlling for the frequency of the noun (which was correlated with how it was tokenized). Of course, the lack of a difference here could just be due to the fact that performance was very high across the board (near 100%). In future work, we’d like to develop a more challenging agreement task, which might reveal differences that were hard to detect in such an easy task.

One of our more interesting findings was that performance was still high even when using an “artificial” tokenization scheme (innovated by Pam) that forced the model to tokenize a word according to its morpheme boundaries. That is, even though the LLM would typically tokenize “mujeres” as “mujeres”, we forced it to represent “mujeres” as the tokens “mujer” and “##es” (both of which already existed in its vocabulary). Even though the model had, by definition, never observed “mujer” and “##es” as a series of tokens in its training data, performance was still very high—suggesting that its representing of “##es” had abstracted something meaningful about plural nouns.

Other work, however, has found a bigger impact of tokenization. This recent preprint, for example, first developed a similar method for identifying whether a word was tokenized according to morpheme boundaries, non-morphemic subwords, or as a single token in the vocabulary. Then, they developed several new benchmarks, which required different English LLMs to match words to definitions, determine the number and type of morphemes in a word, and determine whether two words were semantically related. In each case, the LLM tended to produce better results for words that were tokenized morphologically. The authors write:

…in all language models studied (including ALBERT, BERT, RoBERTa, and DeBERTa), alien tokenization leads to poorer generalizations compared to morphological tokenization for semantic compositionality of word meanings.

(Here, “alien” tokenization refers to words that were parsed into non-morphemic subwords.)

The impact of subword tokenization on model performance is an area of growing interest within research on LLMs. As I wrote above, one particularly important dimension to be aware of here is the fact that languages vary considerably in their morphology. Much is still unknown about the impact of algorithms like BPE on different languages, though this recent paper found that—as expected—BPE learns different kinds of tokens depending on the language in question. Focusing specifically on which subwords are learned first, the authors write:

For languages with richer inflectional morphology there is a preference for highly productive subwords on the early merges, while for languages with less inflectional morphology, idiosyncratic subwords are more prominent.

It remains to be seen whether and how this contributes to disparities in LLMs trained on different languages.

Can tokens look inside themselves?

Another incidental impact of current subword tokenization schemes is that it’s not trivial for a model to “look inside” a given token to know which characters that token contains. After all, if the word “dog” is represented with its own unique ID, it’s not immediately apparently how an LLM could determine that “dog” is spelled “d”, “o”, “g”.

Of course, ChatGPT-4 does a pretty good job figuring out which characters are in a token. If you ask ChatGPT-4 to list out the characters in a word like “inexplicable”, for example, it responds correctly:

ChatGPT-4 knows how “inexplicable” is spelled.

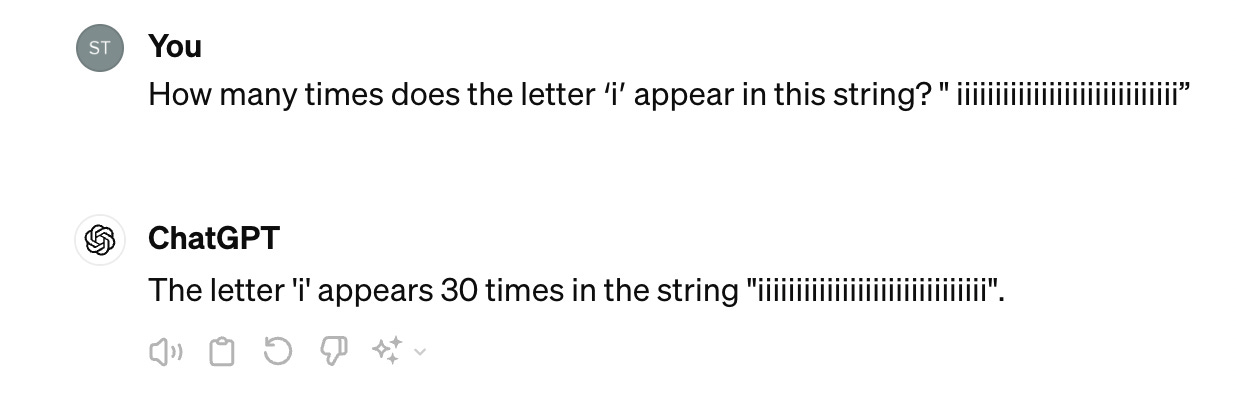
At the same time, there are plenty of examples where even state-of-the-art LLMs struggle to do things that depend on knowing about the individual characters in a string—such as counting how many times a given character occurs. ChatGPT-4 does pretty well on shorter, predictable cases, but one can also devise inputs that trick the model:

ChatGPT overestimates how many times “i” occurs in the string.

In this case, the input string “ iiiiiiiiiiiiiiiiiiiiiiiiiiiii” contains 30 characters, but only 29 of them contain the letter “i”. ChatGPT responds that the letter “i” appears 30 times, and produces a string that does actually contain 30 occurrences of “i”. There are, in fact, many such cases, including cryptic crosswords and ciphers. And as Tom McCoy and others demonstrate in their paper on the “embers of autoregression”, it turns out the LLMs do a better job when the string (or task) in question is more frequent in the LLM’s training data.

Again, this shouldn’t be particularly surprising. LLMs are trained to predict tokens, and if that token contains multiple characters, it’s not clear why or how an LLM should know what those characters are (or how many times each of them occur). I was intrigued, then, when I came across this paper by Ayush Kaushal and Kyle Mahowald on what tokens “know” about their characters.

In that paper, the authors ask whether an LLM’s representations of a token (e.g., for the word “cat”) contains information about the characters in that token (e.g., “c”, “a”, and “t”). To do this, they train a classifier to detect the presence or absence of particular characters (e.g., “c”) in different multi-character tokens—using the embedding for those tokens. Again, there’s not a strong a priori reason to expect that the embedding for “cat” should contain information about how that word is spelled, since “cat” is just represented as a unique ID in the model’s vocabulary. Yet the authors find that all the models tested perform well above chance (50%). Some models, like GPT-J, perform upwards of 80%, meaning that they can accurately detect whether a word contains a given character (e.g., “M”) over 80% of the time. How is this possible?

One possibility is that certain parts of speech are more likely to contain certain characters, and word embeddings already contain information about a word’s part-of-speech. For example, adverbs often end in “-ly”, so if an embedding indicates that a word is an adverb, it should be possible to learn that this word probably contains “l” or “y” (even if not all adverbs end in “-ly”). However, the authors find that predicting which characters are in a word based on the word’s part-of-speech doesn’t perform nearly as well as using the embeddings from GPT-J. A classifier using part-of-speech performs decently (about ~60%) and is above chance, but that can’t be the whole explanation.

Another possibility is that an LLM implicitly learns which characters are in a word because of the fact that the same root word (“lemma”) is sometimes tokenized in different ways, depending on how it is presented. For example, the GPT tokenizer may tokenize the root word “dictionary” as “d + ictionary” (“dictionary), “ dictionary” (“ dictionary”), “d + iction + aries” (“dictionaries”), or “ diction + aries” (“dictionaries”). In theory, it would be useful for the LLM to learn that all these different combinations of tokens are related to the same core meaning (DICTIONARY), and one possible route by which the LLM could do that would be learning something about the overlap in characters across those tokens. The authors write:

We posit that the desirability of learning this mapping is a mechanism by which character information could be learned, by inducing an objective to map between atomic tokens like "dictionary" and the various substring tokens that can arise. While each of these mappings could be learned individually, learning character-level spelling information offers a more general solution to the problem, such that even an entirely novel tokenization could be interpreted by composing the characters of the tokens.

The authors then run a controlled experiment, showing that increasing the variability of how a given word is tokenized (while still keeping this within a reasonable range) actually leads to improved predictions about the characters contained in that word. This is consistent with the hypothesis that some variability in how a root word is tokenized forces the model to learn representations that capture generalizations across those presentations of the word—perhaps similar in principle to the idea that presenting a speech-to-text model with various “noise” conditions forces it to learn more robust representations.

As with the research on morphology, there is a growing body of research on what, exactly, tokens know about their contents: how many letters they have, as well as which vowels and consonants. In my own work, I’ve found that LLMs like GPT-4 can give accurate ratings of how iconic a word is—i.e., whether a word’s meaning is somehow related to how that word sounds. I still haven’t figured out how GPT-4 knows this, but intuitively, answering this kind of question seems to require some kind of knowledge about how a word sounds (and, of course, what a word means).

The future of tokenization

In many ways, subword tokenization is an improvement upon older methods. Tokenizers based on spaces or punctuation (i.e., “word-based tokenizers”) end up with large vocabularies and struggle to handle unknown words—and they also struggle with writing systems that don’t separate words with spaces. Tokenizers based on individual characters are more flexible, but struggle to learn useful, context-dependent representations at higher levels of abstraction (e.g., words or phrases). These days, it seems like subword tokenization results in models that are more robust to out-of-vocabulary words, while also forming representations of words that help with prediction.

It’s still an open question whether and to what extent incorporating information about the morphological structure of words will help language models do their job better. There’s a good chance that the answer to this question will depend on the task in question, and also the language: some languages have richer, more complex morphology than others—and you’d expect morphological information to be more helpful for those languages than for analytic languages like English. This question is complicated further by the fact that there’s still debate among cognitive scientists about exactly how morphology really works in human language comprehension. Do we store morphological knowledge as “rules” or do we mostly just memorize all the different forms of a word? How do these strategies change over the course of development? And is information about rules or stored forms located in different parts of the brain? I’d like to think that future research on this question in humans could inform strategies implemented for language model tokenization—though of course, it’s also possible that different strategies altogether will prove useful for language models.

To me, the biggest question moving forward is how these tokenization strategies impact the performance of models. As we’ve seen, that will require running controlled experiments that compare different approaches to tokenization, and ask how those different approaches affect a model’s performance on some downstream task. The answer could be that for all their differences, most subword tokenization approaches work pretty well on most tasks—but it also might turn out that there are common, clearly identifiable failures modes. We’ll have to do the research to find out.

1. For the sake of this illustrative example, I’ve removed the [CLS] and [SEP] tokens that the BERT tokenizer automatically adds to its input.

2. It’s worth noting that plenty of words don’t have regular morphology. For example, the past tense of “go” is “went”, not “goed”. In fact, many children make errors of overgeneralization when learning a language—such as applying a rule, such as the past tense “-ed”, in a situation where it shouldn’t apply. This is a sign that the child is actually beginning to learn those rules; eventually, they’ll figure out which words are regular (like “walk”) and which are not (like “go”).