Perceptrons, XOR, and the first "AI winter"
A slice of AI history—and why what a system can't do matters.
Contemporary debates about Artificial Intelligence (AI) often center around what an AI system can’t do.
Clearly, AI systems can do many things they couldn’t do in the past. That’s true whether we’re talking about language models passing the bar or systems beating world champions in Go. But they’re also clearly not omnipotent. One reason so many people focus on what they can’t do is that it’s important to know if there are particular categories of behavior or task that are simply impossible for current AI paradigms—or whether success just means more training data and more parameters. A common question, then, looks something like: Will AI system {S} ever achieve capacity {C}, or is there something foundational missing?
I’ll be focusing on this question in a number of upcoming posts—but it’s also notable that this particular flavor of debate has accompanied research in AI since at least the mid-20th century. It’s been an important part of various “hype cycles” of AI, the anti-hype backlashes that inevitably follow, and the occasional “AI Winter”: a period of reduced funding and interest in AI research.1 (It’s also the subject of multiple books by Hubert Dreyfus, including What Computers Can’t Do and What Computers Still Can’t Do).
One of the most important examples in the history of AI begins with the so-called “perceptron”. It’s an illustrative example that also happens to contain some interesting academia drama—and, unfortunately, some real human tragedy.
The first artificial neuron
Back in the 1940s, the mathematician Walter Pitts was introduced to the neurophysiologist Warren McCulloch. Both of them were deeply interested in the connection between biological neurons and logic. At the time, it was understood that biological neurons followed a kind of “all-or-none” principle: if the electrical charge inside a neuron exceeded a certain threshold, the neuron would “fire” (influencing the activity of other neurons it was connected to); if not, the neuron would not fire.
To Pitts and McCulloch, this all-or-none property seemed similar to logic. In principle, they reasoned, a system with binary outputs (ones and zeros) should be able to implement a simple form of propositional logic. A neuron, that is, should be able to represent logical functions like AND and OR. They formalized this analogy in a groundbreaking 1943 paper entitled “A Logical Calculus of the Ideas Immanent in Nervous Activity”.
This was a big deal. AND and OR are two of the foundational functions for logic (and modern computer programming). You can think of them as follows:
AND(X, Y): if both X and Y are True, output True; otherwise output False.
OR(X, Y): if at least one of X and Y is True, output True; otherwise output False.
These functions might sound simple, but if there’s anything we’ve learned from modern computer programming, it’s that you can get a lot of complexity by hooking up relatively simple elements.
So how does an artificial neuron compute these functions?
Here’s a somewhat simplified schematic of how those first artificial neurons worked. Any given “neuron” (the circle) could take an arbitrary number of inputs (here, X1 and X2) and produced a single output (Y). The inputs and the outputs were binary: 1 vs. 0.
The inputs get aggregated in some way using a function g (here, a simple sum). For example, if both inputs are 1, then the aggregated score is 2. Then, a decision function f is applied to that aggregated score, which is meant to be roughly analogous to the thresholding function present in biological neurons. For example, one decision function might say: if the score is greater than or equal to 2, output 1; otherwise, output 0.

What Pitts and McCulloch showed was that this relatively simple system was capable of computing multiple logical functions, such as AND and OR.
To compute AND, the threshold could be set at 2. That means that both X1 and X2 had to be 1, such that their sum was ≥2.
To compute OR, the threshold could be set at 1. That means that at least one of X1 or X2 had to be 1, such that their sum was ≥1.2
Thus, a system inspired by the principles of neuronal activity could provably implement basic logic. Since lots of simple logical functions can be hooked up together to implement more complex functions, that suggested that—again, in principle—lots of these simple “artificial neurons” could be hooked up in networks to implement those functions too. In fact, Pitts and McCulloch demonstrated how many of these “nets” might work in theory in their 1943 paper.
This was very impressive work, and it’s hard to overstate how foundational it was to the field of AI. But it was also “just” a proof-of-concept. There wasn’t (yet) a clear vision for how to implement such a system.
The perceptron: a working model
A little over a decade later, in 1957, Frank Rosenblatt built a working model of an artificial neuron, which he called the “perceptron”. Like the original McCulloch-Pitts design, the perceptron took in “inputs”, applied some activation function to those inputs, and then produced some “output”. For example, a simple output might be a binary decision: “yes” or “no”. (Such a system is called a binary classifier.)
The perceptron’s response (output) for a given set of inputs was determined by weights. A “weight” refers to the strength of the connection each input and the perceptron. In practice, the value of each input is multiplied by the value of its weight. For example, if the input is 2, and the weight is -.5, the result will be -1.

One of the key innovations in Rosenblatt’s implementation was that these weights could be learned from data. “Learning” is an ambiguous word that could mean a lot of different things; here, it just means that each weight starts off randomly, and is iteratively adjusted to make the network’s predictions better and better on a set of training data.
Though words like “perceptron” and “learning” make this process sound quite sophisticated, in practice the early models were not so different from more familiar techniques like linear regression. In linear regression, a model uses a set of inputs “X” and an output “Y” to learn coefficients (or weights) to produce the best-fitting line that relates X to Y. The formula for linear regression actually looks strikingly similar to the aggregation function a a single-unit perceptron might use:

That’s not to diminish the value of Rosenblatt’s accomplishment. In addition to innovating a learning rule for perceptrons, he built a working hardware implementation called the Mark I Perceptron machine (see below). This system had three “layers”. First, an array of 400 light sensors (which Rosenblatt called “S-units”) acted as a kind of “retina”. These S-units were connected to another array of association units (“A-units”), which in turn mapped onto a set of 8 response units (“R-units”).

Rosenblatt’s design was an example of an early image classifier. Modern implementations have, of course, more layers, more complex activation functions, and often more outputs (i.e., more possible “classes” to work with). But the basic intuition is the same.
Initial press releases about the perceptron were extremely enthusiastic. A 1958 article in the New York Times reported that
“the embryo of an electronic computer that [the Navy] expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence.”
Rosenblatt himself was very optimistic about the future of such a system:
“Yet we are about to witness the birth of such a machine – a machine capable of perceiving, recognizing and identifying its surroundings without any human training or control.:
Was all this hype justified?
The language of the press release tends towards anthropomorphism, using words like “embryo” and “be conscious of its existence”. I don’t think most (any?3) theories of consciousness would claim that Rosenblatt’s perceptron was conscious, and it would be many decades before systems built on these principles became useful. At the same time, these were real, genuine advancements. And looking back from 2024, we can see that modern AI systems are, in fact, built on these early foundations.
That said, not everyone at the time was convinced of the potential of these systems.
The skeptics have their say
In 1969, AI researchers Marvin Minsky and Seymour Papert published a book called Perceptrons, in which they argued that the perceptrons built by Rosenblatt (and inspired by Pitts and McCulloch’s initial design) were simply incapable of learning certain functions.
Recall that the artificial neurons described by Pitts and McCulloch could implement logical functions like AND and OR. Crucially, these functions are linearly separable. Roughly, “linear separability” means that if you visualize a bunch of points on a graph, you could draw a straight line separating one category from the other.
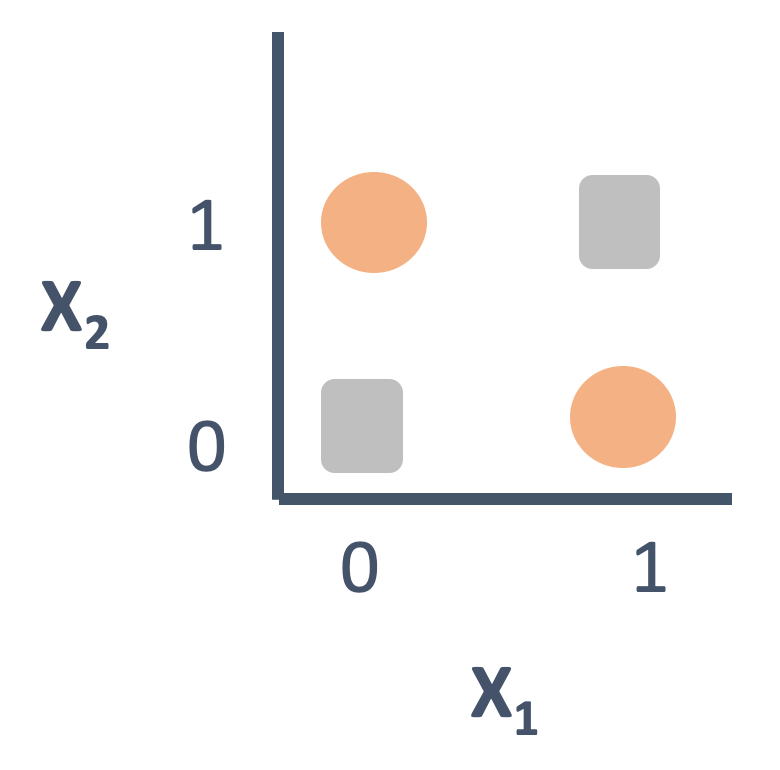
To make this concrete, let’s take a look at a geometric representation of the OR function. The OR function returns 1 (“True”) when at least one of its inputs is 1. In tabular format, then, the OR function would look something like below: when both X1 and X2 are 0, then Y is 0; otherwise, as long as X1 or X2 are 1 (or both are 1), then Y is 1. One way of representing those outputs is in a “truth table”, like the one below:
But we can also draw the same function in a 2-D plane. Here, the position of each point represents its X1 and X2 values, respectively, and the color/shape of that point represents whether its Y value is 0 (gray square) or 1 (orange circle). Note how we can draw a line separating the gray square from the orange circles: that means the OR function is linearly separable.
Now let’s turn to a different function: the XOR (“exclusive or”) function. XOR is true if and only if the inputs are different. That means:
If X1 and X2 are both 0, XOR returns 0.
If X1 and X2 are both 1, XOR returns 0.
But if X1 is 1 and X2 is 0 (or vice versa), XOR returns 1.
If we draw XOR’s truth table on a 2-D plane, we see something quite different from the OR function above:
Unlike the OR function, the XOR function is clearly not linearly separable. There’s no line we can draw in this 2-D plane that will separate all the gray squares from all the orange circles. Of course, we could draw all sorts of non-linear functions to separate these shapes. The point isn’t that there’s no way to separate them; machine learning techniques would soon be developed that could, like support vector machines—and indeed, multi-layer neural networks.
Importantly, however, Minsky and Papert showed that the single-layer perceptrons Rosenblatt had built could not learn the XOR function—or any non-linearly separable function. That placed a sharp upper-bound on the computational power of these single-layer perceptrons. An entire category of functions lay beyond their grasp, calling into question the excitement and enthusiasm present in press releases just a decade before. If neural networks couldn’t learn a basic function, how could we expect one to learn to “walk, talk, see, write, reproduce itself and be conscious of its existence”?
The first “AI winter”
Soon after Perceptrons was published, the first “AI winter” began.
The term “AI winter” is generally used to describe a period of decreased funding or enthusiasm for AI research.4 The period between the early 1970s and the early 1980s saw a sharp reduction in interest for research on neural networks in particular. There’s some debate about exactly to what extent this was driven by Perceptrons in particular, but the book did call attention to key architectural limitations of these models. Minsky and others argued that these models, while impressive on a small scale, would simply never scale up to more complex tasks—they were missing something foundational. Around the same time, there was a surge of interest in alternatives to neural networks, such as so-called “symbolic systems”.5
That meant that many research labs or individual researchers focusing on neural networks lost their funding. Tragically, as was the case for Walter Pitts, some researchers died believing that their life’s work had been for naught. The situation was particularly sad for Pitts, who seems to have experienced considerable decline in his health and personal life towards the end, despite being relatively young (46); apparently, he went so far as to burn his unpublished doctoral dissertation in frustration. (A more detailed, and quite moving, account of Pitts’s life is described in the opening chapters of Brian Christian’s excellent The Alignment Problem.)
Now, looking back, there’s something frustrating about seeing how this played out. Clearly, neural networks nowadays have lots of layers, and they can do a lot more than solve the XOR problem! And even at the time, it was generally understood that perceptrons with multiple layers could solve the XOR problem. But multi-layer neural networks were hard to build and train given other limitations in computational resources; it wasn’t until the discovery of techniques like back-propagation that this became more computationally feasible.
This helps put Minsky’s and Papert’s critique into context. Although it might have been framed (or at least interpreted) as a criticism of neural networks in general, it applied primarily to single-layer perceptrons. As we’ve seen over the last few decades, the criticism obviously did not generalize to larger networks with multiple layers. In hindsight, then, it seems overzealous to call into question the viability of neural network architectures writ large. At the same time, it’s important to remember that researchers didn’t know we’d see such incredible improvements in hardware, or that algorithmic solutions like back-propagation would make training these models easier.
What’s to come?
Remembering these early debates is also helpful for contextualizing contemporary debates about AI systems, such as Large Language Models.
As I mentioned at the beginning of this post, a recurring theme in these debates is the question of whether there are certain things that current systems simply can’t do (and will never be able to do). Candidates I’ve heard in just the last few weeks include “reasoning”, “creativity”, “humor”, and more. It’s entirely possible that these capacities, or some other abilities we haven’t thought of yet, are beyond the scope of LLMs. But I’ll be honest: I find some of these debates frustratingly vague, particularly when compared to the mathematical precision of Perceptrons, which at least was extremely clear about which functions could (i.e., AND and OR) and couldn’t (i.e., XOR) be learned by a single-layer perceptron, and why. I haven’t seen an equally clear formulation of why, architecturally, an LLM should or shouldn’t be able to “reason”. Of course, that doesn’t mean such a formulation doesn’t exist—and if you know of one, please send it to me. But this task seems much harder to me than demonstrating mathematically why single-layer perceptrons cannot solve XOR, in part because “reasoning” is an abstract construct that’s very difficult to operationalize.
Moreover, a problem that afflicts all of these debates is that predicting the future is very hard. Right now, the neural network architecture of choice is the “transformer”, which displays better performance (and is more efficient to train) than older, once popular neural network architectures like recurrent neural networks (RNNs). But it’s possible that a new innovation—either in hardware or software—will make RNNs or RNN-like architectures more popular again. And that’s not to mention the more general question of whether neural networks will (or already have) “hit a wall” (as researchers like Gary Marcus have argued), and whether some alternative approach (e.g., symbolic AI) will come back into style.
We can’t know what will happen. But I’ve found it useful to delve into these aspects of AI history, if only as a reminder of how some questions never really die.
It’s also notable that plenty of people working in or adjacent to the AI space believe another “AI winter” is coming. Whether they’re right, and why, remains to be seen.
In practice, the same result can be achieved by setting a bias term to the artificial neuron (roughly analogous to an intercept in linear regression), so that the threshold can be constant across neuron types.
It’s possible that some approaches, like panpsychism, would allow for a single-unit perceptron to be conscious.
There have been a few winters since the dawn of AI research, and some are even predicting another on the horizon. Predictions in this space tend to be fairly vague and thus hard to falsify, in part because not everyone agrees on what constitutes a “winter”.
The debate between “symbolic” and “connectionist” AI researchers continues to this day, and will be the subject of another post putting AI research in historical context.