Useful cognitive lenses to see through
Tools for thinking.
We do not see the world as it is.
The stuff of experience—perception, cognition, communication—involves a constant grasping for purchase. We’re always seeking a lens through which to see the world better. In these acts we necessarily simplify the world into something human-sized and interpretable. Much complexity is lost in the process, but something valuable is gained: a perspective.
In this post, I’ll discuss some cognitive lenses I’ve found useful for “seeing through”. The important thing is not that any given lens always (or ever) offers the “correct” perspective on an issue—rather, it’s a route through which we gain some kind of conceptual purchase. I’ll also aim to avoid redundancy with related posts, which already mention useful mental models (e.g., “thinking at the margin” and “incentives”).
Many of these concepts, as you’ll see, are actually about frameworks themselves.
Framework #1: Paradigms
To start off with a very meta example: a scientific paradigm is itself a kind of lens through which a particular community of scientists sees through. More specifically, Thomas Kuhn—who helped popularize the notion of a “paradigm shift”—argued that a paradigm is constituted by the various theories, instruments, values, and metaphysical assumptions that guide a group of practicing scientists.
Put another way: which things exist in the world, which things matter, and how ought we measure them? What’s the point of our scientific discipline?
Paradigms are so pervasive they’re sometimes invisible to those inside of them—they’re clearest, in fact, during a paradigm shift, when the underlying assumptions or instruments are called into question. Kuhn describes a number of examples in his book The Structure of Scientific Revolutions. Famous cases in the history of science include the Copernican Revolution (the shift from a geocentric to heliocentric model of the solar system), the germ theory of disease (which overtook miasma theory), and Darwin’s theory of natural selection (replacing older, teleological accounts).
Within my own field of Cognitive Science, a very common (but not universal) paradigm is the notion that the mind is a kind of computer. In this paradigm, minds are understood to be “information processors”, which receive inputs, transduce them into some kind of representation, perform computations over those representations, and then produce an output. Under this paradigm, a major goal is to identify which kinds of representations the mind uses to think—what they look like (are they symbolic or imagistic?), where they come from (are they innate or learned?), and how they are “encoded” in the brain (in individual neurons? in cell assemblies? in particular patterns of spike timing?). The paradigm extends to neuroscience as well: the firing of a neuron is understood to convey information—and different populations of neurons are understood to be sending and receiving information. It also has a direct implication with respect to Artificial Intelligence, which is sometimes taken as intrinsically true as opposed to contingent on the assumptions of the paradigm: namely, that a more powerful computer or information processor (e.g., more operations per second) is also more cognitively capable.
This paradigm was itself a “reaction” (sometimes called the cognitive revolution) to previous approaches to the mind, such as behaviorism, which rejected the notion that we could make suppositions about the goings-on of the mind’s “black box”, and instead focused its efforts on observable behavior. Behaviorists such as B.F. Skinner made incredibly valuable contributions to the field—they’re responsible for concepts like “conditioning”, i.e., learned associations between stimuli and rewards (or punishments). Many of these contributions can be seen as a direct precursor to more modern approaches to Artificial Intelligence, such as reinforcement learning. (Skinner also famously called cognitive science the “creationism” of the mind.)
And although the “mind as computer” paradigm is still fairly dominant within Cognitive Science, it’s by no means the only game in town. There are still behaviorists, for example; and there are also alternate schools of thought, such as enactive cognition, which explicitly rejects the notion of a “mental representation” and urges scientists to understand the mind in terms of the behavior of an entire organism.
I’d argue that paradigms are not limited to science: any community of people has a set of cultural practices and values, as well as implicit (or explicit) ontological commitments. Recognizing those implicit assumptions can be a powerful thing—it’s the first step towards understanding that there are alternative perspectives and that what we call “truth” is in fact more like “contingent, probabilistic assertions”.
Framework #2: Conceptual Metaphor Theory
On the topic of minds: before computers were around, people often understood “the mind” in terms of the dominant technologies of their time. Both Plato and Aristotle compared to the mind to a wax tablet—a device with “inscriptions” that preserve information about the past. Plato also developed the notion of memory as a storehouse (with memories themselves constituted by objects in the storehouse), which, centuries later, Kant extended further: the mind, in this metaphor, was a kind of library (forgotten memories were thus “misplaced books”). The mind, at one point, was even compared to a telephone wire.
These construals of the mind are all metaphors: ways of gaining purchase on a slippery topic by grounding it in something familiar and somehow related. Metaphors are like paradigms, and also like the subject of this post: lenses through which to understand a thing.
In Metaphors We Live By, authors George Lakoff and Mark Johnson argue that metaphor is foundational to human cognition. Far from a mere literary device, metaphor—the construal of one domain (i.e., the “target”) in terms of another (i.e., the “source”)—is a fundamental part of our conceptual system. According to Conceptual Metaphor Theory, these metaphors play a large role in how we understand abstract concepts: we ground them in more concrete, embodied experiences.
First, once you start looking for them, you notice metaphors everywhere in language. Events in time, for example, are often construed as landmarks you pass by (“We’re approaching the holidays”) or as objects approaching you (“The years are shooting by”); relationships are construed as journeys (“We need to talk about where this is going” or “We’ve gone so far together”); ideas are alternately construed as things you exchange (“She gave me a great idea”), things you consume (“I’m still digesting that news article”), or things you see (“This argument is still pretty murky, can you clarify it?”); emotions like anger, as I’ve written about before, can be construed as the build-up of pressure in a container (“He needs to blow off some steam”).
Metaphors are also (often) systematic. Rather than being idiosyncratic, one-off construals, Lakoff and Johnson argued that many of these metaphors form coherent systems, which—much like the grammar of a language—allow you to express novel ideas or make new connections. The “Ideas are Food” metaphor system contains lots of sub-components or “mappings” between those domains:
A poorly thought-out idea is half-baked (or quarter-baked, etc.).
Thinking about an idea is chewing or ruminating on it. (Incidentally, the word ruminate comes from the Latin ruminat, meaning “to chew on”; animals like cows, which chew cud and extract additional nutrients from food, are called ruminants.)
An idea you have trouble agreeing with is one that’s hard to swallow.
Perhaps most crucially, metaphors are not perfect representations of reality. They highlight some features of a concept and obscure others.
For example, the communication of ideas is often construed as a kind of exchange (“She gave me a great idea”). Yet communication doesn’t have all the same properties as exchanging physical objects. Physical objects exist independently of human minds, whereas ideas (by definition) do not. And once you give a physical object to someone else, you no longer possess it; that’s not really true of ideas. These imprecise mappings may also be why it’s so hard to think clearly about domains like intellectual property, or what it means to “own” things like your genes, your digital footprint, and so on—our most concrete experiences with ownership are with physical objects we can hold and exchange, and we’re relying on those experiences to try to “grasp” those more abstract domains.
Metaphors, like paradigms, are the water we swim in. Sometimes, solving a problem is greatly helped by “shifting” the metaphor we’re using to think about that problem. An example in my own research is shifting from thinking about word meanings as “entries” in a kind of “mental dictionary” to being “trajectories” in a “continuous state-space”—neither metaphor is really true in some deep sense, but they highlight different aspects of what meaning is.
Framework #3: Overfitting
Imagine an image classifier is trained to label pictures as DOG or CAT. It’s presented with thousands of pictures of dogs and cats, and over time, learns which features predict DOG vs. CAT. It appears to do a very good job. Then, at one point during its test phase, it is presented with a picture of a dog standing next to a piano; mysteriously, it insists that the label is CAT. Why might this be?
One possibility is that every picture of cats featured a piano. Thus, the classifier might’ve learned a completely spurious association between the label CAT and the presence of a piano (or, even more simply, a sequence of black and white rectangles that correspond to the keys of a piano). In other words, the classifier has overfit to features of its training set that don’t generalize to other observations.
Overfitting is particularly common with very flexible models: the more predictors a statistical model has—the more degrees of freedom it has—the more functions and shapes it can find in a set of data. And although it might end up doing a very good job predicting the data it’s been presented, this might merely be because it’s fit to “noise” in that dataset.
Consider the image below (taken from Wikipedia): if a statistical model has the same number of predictors as data points, it can predict the data perfectly—but the function it learns is likely not at all generalizable to other samples.
Overfitting is a concept from statistics, but I think it ends up being really useful to think about more generally: any time we base our inferences on an unrepresentative sample, we risk overfitting to features of that sample. That’s essentially the argument I made in my recent post on why Cognitive Science needs linguistic diversity. Past research has “overfit” to native English speakers—and in particular, native English speakers enrolled at 4-year research universities.
This extends beyond scientific research as well. Here’s an xkcd with a relevant example. In 1796, it would’ve been correct to assert: “No one without false teeth has ever been elected president of the USA”—yet this is clearly overfitting to the (small) amount of data about past presidents. The comic goes on to list numerous examples that, in retrospect, seem clearly absurd, but which would’ve been literally true of the samples at that time. The lesson is that anytime you’re drawing a generalization from a limited sample, it’s worth asking: am I overfitting to features of this particular sample—or is there a more generalizable principle at work here?
The concept of overfitting also ends up being a useful metaphor (see #2) for thinking about how the brain works. For example, the neuroscientist Erik Hoel has proposed an intriguing theory of why we dream: dreaming, he argues, injects a kind of “noise” into our brain’s training data, preventing it from overfitting to what we perceive in everyday life.
Framework #4: Lumpers vs. splitters
There are many ways to carve up the world. And as we sort things into categories, a question we end up asking is: are X and Y in the same category or different categories? And more generally: how many categories should there be?
In my experience, people’s intuitions about this is often determined by temperament. Hence, the lumper-splitter distinction: some people prefer to sort things into a small number of categories, while others prefer to make fine-grained distinctions.
Here’s an illustrative quote about the distinction by paleontologist George Simpson:
splitters make very small units – their critics say that if they can tell two animals apart, they place them in different genera ... and if they cannot tell them apart, they place them in different species. ... Lumpers make large units – their critics say that if a carnivore is neither a dog nor a bear, they call it a cat.
Dividing organisms into species is a classic example of the lumper-splitter dilemma.
But the problem rears its head in many other domains as well. For example, lexicographers have to ask: when should two usages of the same word be considered distinct meanings (i.e., receive distinct entries in the dictionary)? Does “paint” have the same meaning in “She painted a portrait” vs. “He painted the house” vs. “He painted lines on the street”? What about “He painted a picture with words”? How much of this variation in meaning comes from the context and how much is from distinct mental representations of the word itself?1
Cell biologists have to consider this question too. What’s the most appropriate division of cell types in the brain? One way of dividing neurons is to classify them into inhibitory and excitatory cells; but this leaves out interesting variation in their morphology, spike rates, and underlying genetic profiles. And that variation may be important in understanding how the brain works.
In unsupervised clustering, the problem of determining the “optimal” number of clusters with which to describe a dataset is well-known. On the one hand, you could sort your data points into two, very large clusters—a parsimonious approach, perhaps, but also one that leaves a lot of variation within each cluster. On the other hand, you could adopt an extreme approach where every observation is its own cluster—which minimizes the variance within each “cluster”, but which also ends up simply re-describing your dataset. Not a very useful approach, and quite analogous to the overfitting problem described above. (Borges, as always, has a useful analogy here: a map the size of the territory it represents is not particularly useful.)
There’s not really a single solution here. It ultimately comes down to a few factors:
Your preferences for having a small number of categories vs. capturing fine-grained distinctions.
Which dimensions of variation you think are most important to categorize along.
What your goal is.
Categories are, in the end, a kind of cognitive tool that are meant to serve a purpose. They’re not intrinsic to the world—and lumpers and splitters arguing about where to draw the line would do well to remember that.
Framework #5: The problem of (authoritarian) high modernism
I was first exposed to the concept of “high modernism” in James Scott’s Seeing Like A State. In Scott’s presentation, high modernism is defined by an aspiration to create order in nature and society according to some kind of classification scheme—in other words, to render the world legible in order to control it.
High modernism is not necessarily authoritarian, but does have a tendency towards technocracy (i.e., “let the experts decide”) and easily lends itself towards the kind of top-down planning observed in some authoritarian regimes. It’s also not exclusively “left” or “right”. And finally, high modernism is everywhere—it’s easy to point to past examples and laugh at the follies of overly zealous planners, but high modernism is the (often very well-intentioned, and perhaps even correct) animating impulse behind pretty much any policy that’s designed to restructure or reorganize society.
I think the failure modes of high modernism are probably clearest with examples, which Scott’s book is full of.
One of my favorite examples is “scientific forestry”. In 18th-century Germany, a wood shortage threatened the economy. To try to rectify the situation, mathematicians and policy makers at the time identified the “optimal” tree—i.e., an idealized “tree-unit” (called a Normalbaum) that would produce an optimal number of timber per square unit of forest. This allowed them to create a model of the ideal forest, which, far from the chaotic old-growth forests of the time, was a more grid-like and legible structure full of identical trees with predictable yields. Thus, scientific forestry was born, and indeed, for at least the first generation of these scientifically managed forests, the yields were fantastic.
But the cracks in the scheme started showing by the second and third generation: this monocropping ended up being a disaster for local peasants, who relied on forest diversity for grazing, medicines, and so on; additionally, the genetic homogeneity of these “tree-units” rendered them much more susceptible to disease, as well as storms (since they were all the same height); and an absence of under-brush led to thinner and less nutritious soils (i.e., depleting the “soil capital”). These issues ultimately required further intervention in the form of a managed “forest hygiene”: foresters had to replace (often artificially) many of the chaotic elements they’d previously abstracted away from the forest’s diversity—for example, they replaced hollow trees (previously home to owls and woodpeckers) with specially designed wooden boxes, reintroduced spiders, and designed new ant colonies.
As Scott writes, this example highlights the:
dangers of dismembering an exceptionally complex and poorly understood set of relations and processes in order to isolate a single element of instrumental value.
The rest of Seeing Like a State is essentially a long tour of the dangers of abstraction and the quest for legibility. The history of human societies, it seems, is full of institutions (often states) trying to create standardized measurement schemes—typically in an effort to control the population or harness additional revenue from them (e.g., through taxes).
And critically, once these schemes are introduced, they can terraform the very landscape—often simplifying it in ways that make it easier to measure, such that the simplifying abstractions end up becoming true by virtue of this iterative process.
I find myself turning to this concept of legibility frequently. Examples abound in education: GPA and standardized tests are both attempts to measure latent properties in a population (i.e., students) in order to assess their own potential and the quality of the education they’ve received. Even when designing my assessments, I find myself terraformed by the tools I have available. Certain assessment styles might be hard to implement at scale, or in platforms like Canvas; thus, I am led, even if only slightly, towards approaches that are easier to design.
Another modern example is Search Engine Optimization (SEO): everyone wants their web page to show up in a Google search, so they design the content in such a way that Google’s algorithm ranks it highly. This, apparently, is one reason why so many food recipes begin with a lengthy description rather than jumping right to the recipe itself.
Ultimately—at least in my view—there’s nothing “wrong” with searching for abstractions that make the world more comprehensible. It’s perhaps the primary goal of science. But Seeing Like a State reminds us of the costs of abstraction (see also #4 above). Particularly in an increasingly designed world, I worry about terraforming away the complexities that give life its rich texture and meaning.
If you’re interested in this, I’ve explored the issue in past posts as well2:
Framework #6: Considering the Counterfactual
This newsletter is called The Counterfactual, though I’ve so far written strikingly little about what I intended to be a central theme.
No number stands alone. Evaluating claims requires some kind of comparison or context. Suppose someone tells you the United States spends about $33B a year on foreign aid. Is that a lot? A little? Many Americans (57%), when asked, think that the USA spends too much on foreign aid. However, they also tend to vastly overestimate what percentage of the total budget goes towards foreign aid: in one survey, the average guess was approximately 27%—but the real number is less than 1%. Put in context, this is considerably less than spending on national defense (about 12% of 2022 spending), social security (about 19% of 2022 spending), and health (about 15% of 2022 spending).
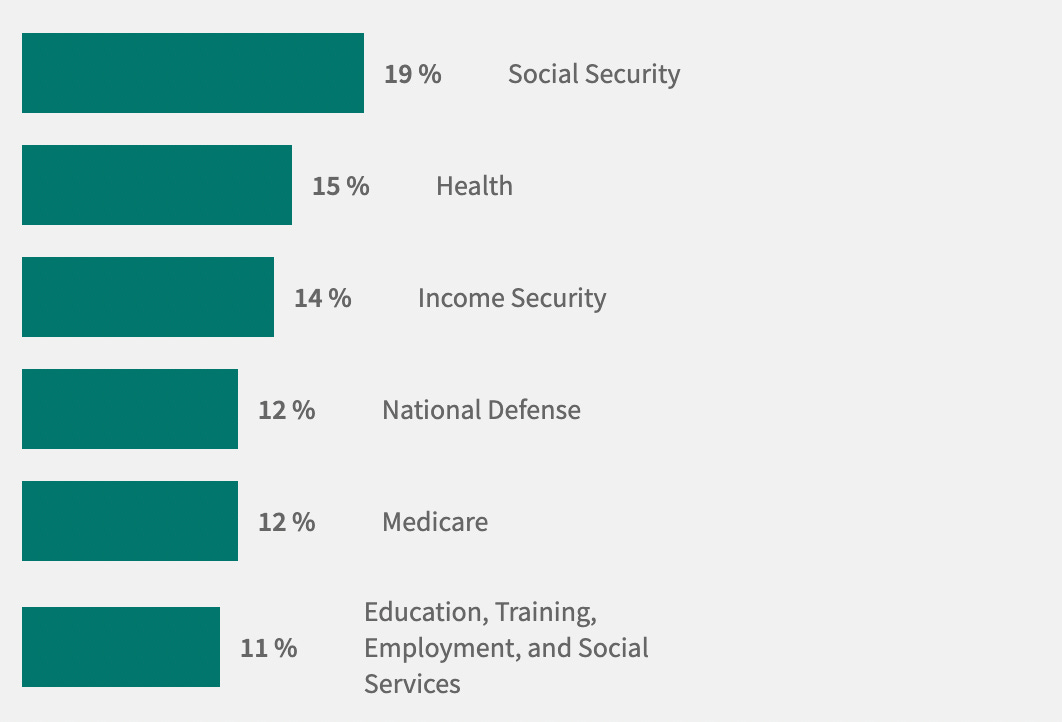
Knowing how much a country spends on defense vs. social security vs. foreign aid doesn’t tell us how much they should spend; that’s a debate about values, and reasonable people can disagree. But that debate needs to be grounded in empirical data: to evaluate how much to spend on one category, we need to know how much we spend on other categories.
This example highlights a simple but helpful approach to evaluating claims, which I sometimes call “Compared to what?”, and which others have called “Is that a big number?”
But thinking with counterfactuals includes more than just numerical claims. For example, any time we make (or evaluate) a claim about the efficacy of some intervention, we have to compare that intervention to a range of other plausible interventions—including not intervening at all. Here are some brief examples:
In Triumph of the City, the economist Ed Glaeser talks about this issue with respect to the burdensome regulations (e.g., California’s CEQA) that often hinder building and development in cities. Blocking a dense apartment building or transit line may feel like a win to some, but it neglects the fact that this obstruction will only shift demand (either for housing, or for other means of transit, e.g., cars) onto other parts of the system—perhaps incurring much higher emission costs overall. If people considered the counterfactual—what the costs of building vs. the costs of not building—perhaps they’d realize this.
Tyler Cowen has written extensively about sins of “commission” vs. sins of “omission”. Sins of omission (e.g., not moving fast enough to approve the COVID vaccines) are often tolerated, while sins of commission (e.g., moving too quickly to approve the COVID vaccines) are often punished. This arguably stems from a lack of counterfactual thinking as well.
The well-known “Regression fallacy” is borne out of an analyst’s failure to consider regression to the mean. Suppose an educational intervention is implemented in the counties with lowest reading performance; the next year, reading scores in those counties improves. Success? Based on this design, it’s impossible to know—regression to the mean predicts that, on average, scores in those worst counties would’ve improved regardless. Without a control group, we don’t know whether the intervention improved scores more than expected; it’s possible it even hurt them.
To be clear, I am not the first person to note that it’s important to consider the counterfactual. It’s the entire motivation behind null hypothesis testing—i.e., how likely is a given statistical result under the “null hypothesis” (essentially a formalization of the possible world in which the null hypothesis is true). Its also the motivation behind randomized controlled trials (or “RCTs”): randomly assigning participants to different experimental conditions essentially manufactures two miniature worlds that are as closely controlled as possible, except for the key manipulation of interest—allowing researchers to compare two counterfactual scenarios.
But I do think that many debates, and many people (myself very much included), benefit from trying to spell out the underlying assumptions behind an argument as explicitly as possible; and that includes the counterfactual scenarios or comparisons under consideration.
I’ll discuss this issue at greater length in an upcoming post, along with a recent paper I published tackling the question.
I’ll also be discussing it at more length in an upcoming essay on the Metaverse.

